Nerd Squared : A Saturn V Rocket Built By Harry Potter

I am a huge Harry Potter fan. When I was 12 or 13, I got a Harry Potter trivia game for Christmas. When I was asked what flavor popsicle Harry ate when he went to the zoo with the Dursleys, I not only knew the answer. I was able to look up the page in the book to prove to my brother that Harry had a lemon popsicle, not a cherry flavored popsicle as the trivia game incorrectly claimed. From that moment on, no one would play that game with me.

Now that I am studying math and physics, I was naturally interested in some of the math and physics behind Harry Potter. I was really intrigued with broomsticks. The other day, some information from a Harry Potter book caught my eye. In the Prisoner of Azkaban, the Firebolt broomstick's top speed is advertised as 150mph (or 67m/s) and can accelerate to that speed in 10 seconds.

Acceleration is a measurement of the change in velocity relative to the change in time. It is equal to the change in velocity divided by the change in time, so we can calculate that the acceleration of the broom is (67 m/s)/(10 sec) or 6.7m/s². I looked at Amazon's shipping information to find out how much the average broom weighs. A typical broom weighs about 1 pound, or 0.5kg. Daniel Radcliffe (the actor who plays Harry Potter) has a listed mass of 53kg.

Since Force = Mass * Acceleration, we know that the amount of thrust produced by one Firebolt is equal to (6.7m/s²) * (53.5kg), or around 360 Newtons.

While this is an interesting factoid, knowing the amount of thrust that something produces doesn't really mean a whole lot without any context. I wanted to compare the thrust to the amount of thrust that other vehicles can create to really get a sense of how powerful these broomsticks are.

What I found would probably surprise no one. Cars, boats, planes, and rockets can all produce much more thrust than a broomstick. But a broomstick weighs so much less than these other objects! If we had the same mass of broomsticks as the mass of whatever is powering the craft, I'm sure the broomsticks would dominate! So let's look at that.

I wanted to look at the most extreme example I can find: the Saturn V Rocket.

Weighing in at a whopping 5 million pounds, this world heavy weight champion of spaceflight was used to fly the Apollo missions to the moon. This rocket used 2,160,000 kg of liquid oxygen and liquid hydrogen as rocket fuel and produced a thrust of 7.5 million pounds (or 3.4*10⁷ Newtons). The first stage of the engine burned for 168 seconds, at which time the rocket was at an altitude of 67,000 meters and was moving 2,300 m/s.

OK, there are many different ways to compare the NASA model and the HP model. If we just straight up traded the mass of fuel for the mass of broomsticks, we would have around 4,320,000 broomsticks. At the rate of 360 Newtons/broomstick, this would create 1.6*10⁹ Newtons of thrust, easily surpassing the liquid oxygen and hydrogen.

Or we could figure out how many brooms we would need to create the amount of thrust needed. We still have 360 Newtons/broom, so 3.4*10⁷ Newtons requires 95,000 brooms. Cool!

But this doesn't really tell the full story. One of the main reasons rockets are so heavy is because they have to carry their fuel with them. They start out extra heavy and end up with hardly any mass left. But if we used broomsticks, that mass would not change. NASA is all about efficiency, and any good Quidditch player doesn't want to waste any broomsticks. So we want to figure out the minimum number of brooms to reach the stars.

Remember that brother that refused to play Harry Potter trivia that I talked about above? He's now a rocket scientist. He got his undergraduate and graduate degrees in Aerospace and Mechanical Engineering at the University of Michigan (Go Blue!) and now works as an engineer at Boeing, so I naturally tagged him in for this fight.

I'd recommend using a Fourier Transformation then finishing it off with a Suplex.

He was very intrigued. You see, the really tricky part about rockets is that they require a LOT of fuel. They are constantly burning a massive amount of fuel, so the mass you end up with is very different from the mass you start with. My brother said that engineers normally deal with Tsiolkovsky's equation, which is:

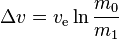
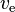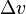where  is the velocity of the exhaust,  is the initial mass (both rocket and fuel),  is the final mass, and  is the maximum change in velocity of the craft. Since we are using magic to power our rockets, there is no change in mass.

This means that m/m above is equal to 1, and as we all know after looking at logarithmic functions, the logarithm of 1 is equal to 0. Therefore according to Tsiolkovsky, we cannot move.

My brother told me that since rockets are so aerodynamic and stable, we don't really need to worry about the drag force acting on the rocket. Rockets are specifically engineered to minimize the air resistance, which means that the drag force is significantly less than the amount of thrust produced by the rocket.

This is pretty much word for word how I asked my brother for help.

So this problem breaks down to a simpler-than-you-would-expect-for-rocket-science-meets-magic scenario. Since we don't have to worry about changing mass or drag forces, we only have 2 forces acting on the rocket: gravity and thrust. We know that these two forces added together equal the net force, and the net force needs to be great enough to get the rocket up to escape velocity (which is 11,200 m/s).

Force_Net = Force_Thrust - Force_Gravity

mass*v_esc/t = (360 Newtons/Broom)*(n brooms) - mg

(120,000+n/2 kg)(11,200 m/s)/(168 sec) = (360 N/broom)n - (120,000+n/2 kg)(9.81 m/s²)

33.3n + 8*10³ = 360n - 4.9n - 1.2*10⁶

322n = 1.208*10⁶

n = 28,500 brooms

So it would take about 28,500 Firebolt broomsticks to fly the Saturn V rocket into outer space. This seems like a lot, but is it?

The Saturn V rocket uses about 90,000 kg of liquid hydrogen, 1,800,000 kg of liquid oxygen, and 700,000 kg of RP-1 (rocket propellant 1, similar to kerosene). This fuel costs around $800,000 today. Meanwhile, the Firebolt broomstick cost around 1000 galleons in the Harry Potter books in 1993. This converts to about $10,000 in 1993 or $16,500 in 2014. This means that the total cost of the brooms would be 28,500*$16,500, or about $470 million.

Unfortunately this method of space travel would not save us money until about our 590th trip into space. While it might start getting more cost effective if we started sending spaceships farther out into space, for the immediate future it would not save us money. I say we go for it even though it costs more. I think half a billion dollars is a fair price to kick the laws of nature in the face!